Grouped Parameters

This example is to demonstrate syntax and flexibility of using parameter groups along with the Numpy mathematic library for advanced parameterization.

The Problem

Consider the below setup. There is an airfoil, for which I want to apply a force load on the end. In the initial setup, the force load is in the negative Y axis direction. However, I want to sweep the angle of this vectory in the XY plane from -45˚ to +45˚ from it’s current vertical position over 20 simulations.

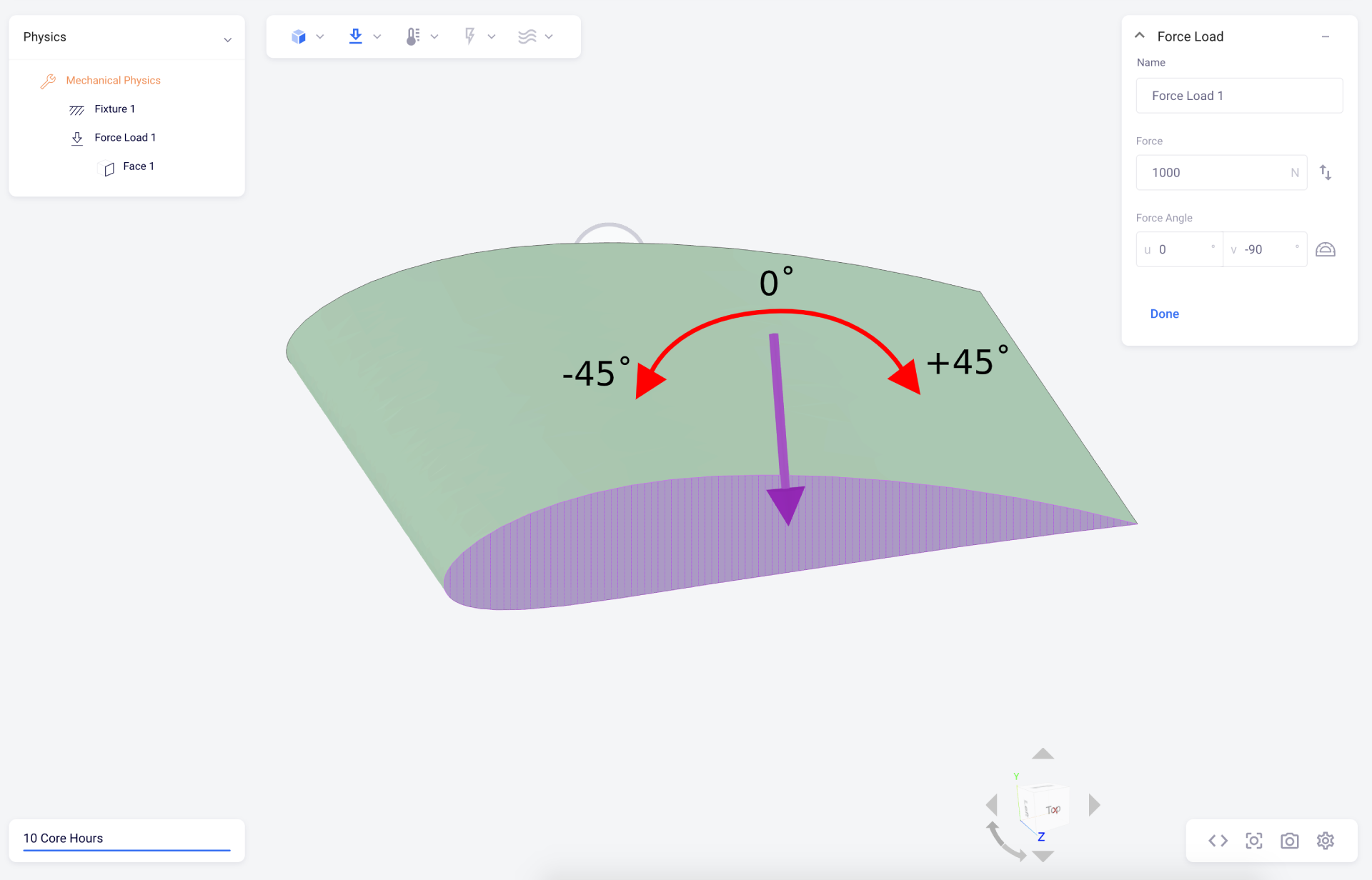
image info

Initial Code

import onscale as on

with on.Simulation('Airfoil-Stress') as sim:

    geometry = on.CadFile('Airfoil.step')

    materials = on.CloudMaterials('onscale')
    aluminum = materials['Aluminum']
    aluminum >> geometry.parts[0]

    force = on.loads.Force(1000, [0, -1, 0])
    force >> geometry.parts[0].faces[1]

    restraint = on.loads.Restraint(x=True, y=True, z=True)
    restraint >> geometry.parts[0].faces[0]

    on.fields.Displacement()
    on.fields.Stress()
    on.fields.Strain()
    on.fields.VonMises()
    probe = on.probes.ResultantForce(geometry.parts[0].faces[0])

The Solution

The issue with defining this sweep is that two values need to be parametrized simultaneously, both the x and y component of the on.loads.Force vector.

import onscale as on

with on.Simulation('Airfoil-Stress') as sim:

    param_x = # ???
    param_y = # ???

    force = on.loads.Force(1000, [param_x, param_y, 0])

We can start by defining our \(`x`\) and \(`y`\) components in terms of our sweep angle \(`\theta`\) using Numpy:

import numpy as np

min_theta = -np.pi / 4
max_theta = np.pi / 4
theta = np.linspace(min_theta, max_theta, 20)
x = -np.sin(theta)
y = -np.cos(theta)

print("X:", x)
print("Y:", y)

X: [ 0.70710678  0.64629924  0.58107682  0.51188505  0.43919659  0.36350797
  0.28533622  0.20521534  0.12369263  0.04132497 -0.04132497 -0.12369263
 -0.20521534 -0.28533622 -0.36350797 -0.43919659 -0.51188505 -0.58107682
 -0.64629924 -0.70710678]
Y: [-0.70710678 -0.76308407 -0.81384872 -0.85905395 -0.89839098 -0.93159109
 -0.95842748 -0.97871685 -0.99232058 -0.99914576 -0.99914576 -0.99232058
 -0.97871685 -0.95842748 -0.93159109 -0.89839098 -0.85905395 -0.81384872
 -0.76308407 -0.70710678]

Explanation:

Define our minimum angle -45˚ or \(`-\frac{\pi}{4}`\)
Define our maximum angle 45˚ or \(`\frac{\pi}{4}`\)
Create a linear sweep of 20 points between these two angles \(`\theta`\)
Recover the \(`x`\) and \(`y`\) components using trig functions

Note: The trig functions are negative since our vectory is in the \(`-y`\) direction, and we use \(`\cos(y)`\) instead of \(`\sin(y)`\) since our 0˚ corresponds to the \(`y`\) unit vector.

To verify our sweep is correct, let’s plot the vectors using Matplotlib:

import matplotlib.pyplot as plt

plt.quiver(x, y, scale=10)

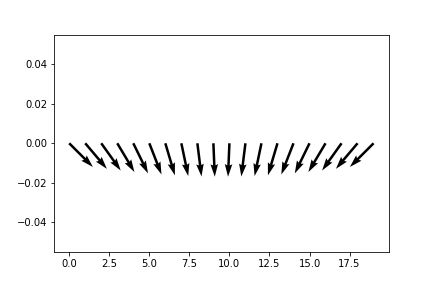
image info

That’s exactly what we expected. Now to use the x and y arrays we generated as parameter sweeps, we can use the onscale.parametrize function to automatically generate grouped parameters from our arrays:

import numpy as np
import onscale as on

min_theta = -np.pi / 4
max_theta = np.pi / 4
theta = np.linspace(min_theta, max_theta, 20)
x = -np.sin(theta)
y = -np.cos(theta)

with on.Simulation('Airfoil-Stress') as sim:

    param_x, param_y = on.parametrize(x, y)
    force = on.loads.Force(1000, [param_x, param_y, 0])

And that’s it! The on.parametrize turns our arrays into parameters that are grouped, meaning that our simulation sweep with iterate over them together (instead of taking all possible combinations of x and y). We will now get a 20-simulation sweep of our desired force loads.

Final Code

import numpy as np
import onscale as on

min_theta = -np.pi / 4
max_theta = np.pi / 4
theta = np.linspace(min_theta, max_theta, 20)
x = -np.sin(theta)
y = -np.cos(theta)

with on.Simulation('Airfoil-Stress') as sim:

    param_x, param_y = on.parametrize(x, y)

    geometry = on.CadFile('Airfoil.step')

    materials = on.CloudMaterials('onscale')
    aluminum = materials['Aluminum']
    aluminum >> geometry.parts[0]

    force = on.loads.Force(1000, [param_x, param_y, 0])
    force >> geometry.parts[0].faces[1]

    restraint = on.loads.Restraint(x=True, y=True, z=True)
    restraint >> geometry.parts[0].faces[0]

    on.fields.Displacement()
    on.fields.Stress()
    on.fields.Strain()
    on.fields.VonMises()
    probe = on.probes.ResultantForce(geometry.parts[0].faces[0])

Under the Hood

The on.parametrize is a convenience method for turning arrays into grouped parameters. In the example we used just 2 input arrays, but the function actually accepts an arbitrary number of arrays:

import numpy as np
import onscale as on

x = np.linspace(0, 2 * np.pi, 100)
y = np.cos(x)
z = np.sin(x)

with on.Simulation('demo') as sim:

    px, py, pz = on.parametrize(x, y, z)

As long as all arrays passed to on.parametrize are the same length, we get back one parameter for each array. The above code will expand to:

import numpy as np
import onscale as on

x = np.linspace(0, 2 * np.pi, 100)
y = np.cos(x)
z = np.sin(x)

with on.Simulation('demo') as sim:

    px = on.CustomParameter('custom_1', x)
    py = on.CustomParameter('custom_2', y)
    pz = on.CustomParameter('custom_3', z)
    group = on.ParameterGroup()
    px >> group
    py >> group
    pz >> group

Any array of values can be made into a simulation parameter with CustomParameter. By default, these three each have 100 values, which would result in \(`100^3 = 1000000`\) simulations of all possible combinations. If we create a ParameterGroup and group them together, we instead will iterate over the zipped 100 values together.